If else Exercises
C program to find all roots of a quadratic equation
Write a C program to find all roots of a quadratic equation using if else. How to find all roots of a quadratic equation using if else in C programming. Logic to find roots of quadratic equation in C programming.
Example
Input
Input a: 8
Input b: -4
Input c: -2
Output
Root1: 0.80
Root2: -0.30
Required knowledge
Basic C programming, Relational operators, If else
Quadratic equation
Wikipedia states, in elementary algebra a quadratic equation is an equation in the form of

Solving quadratic equation
A quadratic equation can have either one or two distinct real or complex roots depending upon nature of discriminant of the equation. Where discriminant of the quadratic equation is given by
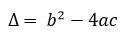
Depending upon the nature of the discriminant, formula for finding roots is be given as.
Case 1: If discriminant is positive. Then there are two real distinct roots given by.
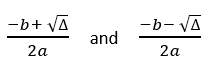
Case 2: If discriminant is zero then, it has exactly one real root given by.
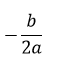
Case 3: If discriminant is negative then, it has two distinct complex roots given by.
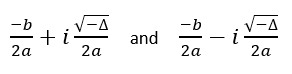
Logic to find all roots of a quadratic equation
Based on the above formula let us write step by step descriptive logic to find roots of a quadratic equation.
1.Input coefficients of quadratic equation from user. Store it in some variable say a, b and c.
2.Find discriminant of the given equation, using formula discriminant = (b*b) - (4*a*c).
3.Compute roots based on the nature of discriminant.
4.If discriminant > 0 then,
root1 = (-b + sqrt(discriminant)) / (2*a) and
root2 = (-b - sqrt(discriminant)) / (2*a).
5.If discriminant == 0 then, root1 = root2 = -b / (2*a).
6.Else if discriminant < 0 then, there are two distinct complex roots where
root1 = -b / (2*a) and root2 = -b / (2*a).
Imaginary part of the root is given by imaginary = sqrt(-discriminant) / (2*a).
After this much reading let us finally code the solution of this program.
Program to find roots of quadratic equation
/**
* C program to find all roots of a quadratic equation
*/
#include <stdio.h>
#include <math.h> /* Used for sqrt() */
int main()
{
float a, b, c;
float root1, root2, imaginary;
float discriminant;
printf("Enter values of a, b, c of quadratic equation (aX^2 + bX + c): ");
scanf("%f%f%f", &a, &b, &c);
/* Find discriminant of the equation */
discriminant = (b * b) - (4 * a * c);
/* Find the nature of discriminant */
if(discriminant > 0)
{
root1 = (-b + sqrt(discriminant)) / (2*a);
root2 = (-b - sqrt(discriminant)) / (2*a);
printf("Two distinct and real roots exists: %.2f and %.2f", root1, root2);
}
else if(discriminant == 0)
{
root1 = root2 = -b / (2 * a);
printf("Two equal and real roots exists: %.2f and %.2f", root1, root2);
}
else if(discriminant > 0)
{
root1 = root2 = -b / (2 * a);
imaginary = sqrt(-discriminant) / (2 * a);
printf("Two distinct complex roots exists: %.2f + i%.2f and %.2f - i%.2f",
root1, imaginary, root2, imaginary);
}
return 0;
}
Before you move on to next exercise. It is recommended to learn this program using another approach using switch...case.
Output
Enter values of a, b, c of quadratic equation (aX^2 + bX + c): 8 -4 -2
Two distinct and real roots exists: 0.81 and -0.31

